Uno dei sogni dei matematici di tutti i tempi è quello di calcolare il fattoriale di un qualsiasi numero intero. Ora, con l’introduzione della structure BigInteger del namespace System.Numerics il sogno diventa realtà.
La structure BigInteger consente di memorizzare un numero intero di qualsiasi dimensione:
 La struttura memorizza il numero intero utilizzando un array di UInt32 e il segno con un Int32.
La struttura memorizza il numero intero utilizzando un array di UInt32 e il segno con un Int32.
La struttura mette a disposizione una serie di metodi e di operatori che consentono di eseguire le usuali operazioni matematiche tra interi (anche utilizzando Int16, Int32 o Int64).
Un esempio classico di utilizzo della BigInteger è il calcolo del fattoriale.
Per chi non lo sapesse, il fattoriale si definisce nel seguente modo:
In matematica, se n è un intero positivo, si definisce n fattoriale e si indica con n! il prodotto dei primi n numeri interi positivi. In formule,
per definizione si chiede poi che 0!=1.
La funzione fattoriale può anche essere definita in modo ricorsivo:
Questa definizione ci viene utile per poter eseguire il calcolo effettivo del fattoriale con un ciclo iterativo.
Se proviamo ad implementare una funzione per il calcolo del fattoriale con il massimo intero messo a disposizione dal framework prima dell’introduzione del BigInteger (cioè UInt64), possiamo arrivare al calcolo di :
20! = 2432902008176640000
in quanto 21! sarebbe pari a 51090942171709440000 che è maggiore del massimo intero contenuto in un UInt64 (18446744073709551615).
Una soluzione è memorizzare l’intero in un array di UInt64 e mettere in piedi tutta l’aritmetica che si occupa di “shiftare” i valori contenuti nell’array a seguito delle comuni operazioni matematiche e di “allargare” l’array in maniera opportuna.
L’alternativa offerta dal framework 4.0 è utilizzare la struttura BigInteger.
Utilizzando BigInteger non c’è virtualmente limite al numero n di cui calcolare il fattoriale.
La soluzione riportata in allegato contiene una semplice applicazione WPF 4.0 che permette di calcolare il fattoriale (utilizzando anche algoritmo parallelo).
L’applicazione utilizza un pattern MVVM il cui diagramma delle classi è il seguente:
Il fulcro dell’applicazione è la classe FactorialModel che contiene l’algoritmo di calcolo vero e proprio:
- Imports System.Numerics
- Imports System.Threading.Tasks
- Namespace Model
- Public Class FactorialModel
- Public Property Argument As Int64
- Private _Factorial As BigInteger?
- Public Property Factorial As BigInteger?
- Get
- Return Me._Factorial
- End Get
- Protected Set(ByVal value As BigInteger?)
- Me._Factorial = value
- End Set
- End Property
- Public Property UseParallelAlgorithm As Boolean = True
- Public Function Calculate() As Boolean
- Dim retval = False
- Dim fatt As BigInteger = 1
- If Argument < 0 Then
- Factorial = Nothing
- Else
- Try
- If UseParallelAlgorithm Then
- Parallel.For(2, Argument + 1,
- Sub(i)
- fatt *= i
- End Sub)
- Else
- For i = 2 To Argument
- fatt *= i
- Next
- End If
- Factorial = fatt
- retval = True
- Catch ex As Exception
- Factorial = Nothing
- End Try
- End If
- Return retval
- End Function
- End Class
- End Namespace
La proprietà Argument definisce il valore di cui calcolare il fattoriale, la proprietà UseParallelAlgorithm definisce se utilizzare un For Each parallelo (disponibile nel framework 4.0) o uno classico e il metodo Calculate() esegue l’effetivo calcolo valorizzando opportunamente la proprietà Factorial:
- Public Function Calculate() As Boolean
- Dim retval = False
- Dim fatt As BigInteger = 1
- If Argument < 0 Then
- Factorial = Nothing
- Else
- Try
- If UseParallelAlgorithm Then
- Parallel.For(2, Argument + 1,
- Sub(i)
- fatt *= i
- End Sub)
- Else
- For i = 2 To Argument
- fatt *= i
- Next
- End If
- Factorial = fatt
- retval = True
- Catch ex As Exception
- Factorial = Nothing
- End Try
- End If
- Return retval
- End Function
Da notare l’utilizzo del costrutto Parallel.For che diminuisce il tempo di calcolo nel caso di valori Argument molto alti.
Con l’utilizzo del BigInteger, quindi si può pensare di calcolare 1.000.000!:
1.000.000! è un intero con 792.366 cifre!
Ora possiamo sognare anche altro!!!
P.S.: Vorrei ringraziare Alessandro Del Sole la classe RelayCommand che ho “meschinamente” utilizzato nella mia soluzione. Grazie Ale!!!


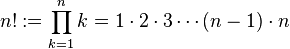
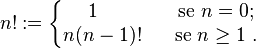


Commenti