Vorrei segnalarvi che nella versione 4.0 del framework è stato introdotto un nuovo namespace, chiamato System.Numerics, contenente dei tipi numerici che fino ad ora mancavano all’interno del framework: i numeri complessi e gli interi di dimensione non definita.
In questo post ci occupiamo dei numeri complessi.
Prima di vedere come sono implementati nel framework, vorrei richiamare alcuni concetti matematici.
I numeri complessi sono un'estensione dei numeri reali nata inizialmente per consentire di trovare tutte le soluzioni delle equazioni polinomiali. Ad esempio, l'equazione
non ha soluzioni reali, perché in questo insieme non esistono numeri il cui quadrato sia negativo.
Si definisce allora il valore i, chiamato anche unità immaginaria, che gode della seguente proprietà:
e dunque:
I numeri complessi sono formati da due parti, una parte reale ed una parte immaginaria, e sono rappresentati dalla seguente espressione:
dove a e b sono numeri reali, mentre i è l'unità immaginaria.
Per maggiori info di carattere matematico http://it.wikipedia.org/wiki/Numero_complesso
Il framework implementa i numeri complessi tramite la struttura Complex.
 La struttura mette a disposizione 4 proprietà:
La struttura mette a disposizione 4 proprietà:
- Imaginary : è un double che contiene la parte immaginaria del numero complesso;
- Magnitude : è il raggio del numero complesso rappresentato in forma polare;
- Phase : è l’angolo del numero complesso rappresentato in forma polare;
- Real : è un double che contiene la parte reale del numero complesso.
Abbiamo, inoltre, a disposizione tutta una serie di operazioni matematiche che accettano, oltre che argomenti di tipo Complex, anche argomenti numerici preesistenti come Double, Integer, etc., etc.
La struttura ci mette, infine, a disposizione tre attributi statici che forniscono il prototipo dell’unità, dell’unità immaginaria e dello zero.
Un esempio pratico di utilizzo della struttura Complex è il calcolo delle soluzioni di un’equazione di secondo grado nella forma:
Il progetto allegato al post è formato da una semplice windows WPF, un model che si occupa del calcolo delle soluzioni dell’equazione di secondo grado e un viewmodel che si occupa di collegare il model alla window.
Non analizzeremo il viewmodel concentrandoci sulla classe EquationModel che contiene la logica di calcolo.
- Imports System.Numerics
- Namespace Model
- Public Enum EquationType
- Undefined
- FirstDegree
- SecondDegree
- End Enum
- Public Class EquationModel
- Public Property A As Double
- Public Property B As Double
- Public Property C As Double
- Public ReadOnly Property Delta As Double
- Get
- Return (Math.Pow(B, 2) - 4 * A * C)
- End Get
- End Property
- Public ReadOnly Property Type As EquationType
- Get
- If A = 0 Then
- If B = 0 Then
- Return EquationType.Undefined
- Else
- Return EquationType.FirstDegree
- End If
- Else
- Return EquationType.SecondDegree
- End If
- End Get
- End Property
- Public ReadOnly Property X1 As Complex?
- Get
- Dim x As Complex?
- Dim y As Complex?
- CalculateSolutions(x, y)
- Return x
- End Get
- End Property
- Public ReadOnly Property X2 As Complex?
- Get
- Dim x As Complex?
- Dim y As Complex?
- CalculateSolutions(x, y)
- Return y
- End Get
- End Property
- Private Sub CalculateSolutions(ByRef x1 As Complex?, ByRef x2 As Complex?)
- x1 = Nothing
- x2 = Nothing
- If A = 0 Then
- If B <> 0 Then
- x1 = -C / B
- x2 = x1
- End If
- Else
- x1 = (-B + Complex.Sqrt(Delta)) / (2 * A)
- x2 = (-B - Complex.Sqrt(Delta)) / (2 * A)
- End If
- End Sub
- End Class
- End Namespace
La classe espone i tre coefficienti dell’equazione (A, B e C) e alcune proprietà calcolate:
- Delta : la quantità delta che viene utilizzata nel calcolo delle soluzioni;
- Type : tipo effettivo dell’equazione (non definita, di primo grado, di secondo grado);
- X1, X2 : soluzioni dell’equazione. Queste proprietà sono di tipo Complex? poichè non è detto che l’equazione abbia soluzioni (ad esempio A=0, B=0 e C=1 non ha soluzioni).
Il metodo privato CalculateSolutions() è il metodo utilizzato per il calcolo effettivo delle soluzioni. All’interno di questo metodo possiamo osservare l’utilizzo del metodo Sqrt() della struttura Complex per il calcolo della radice quadrata.
Il diagramma delle classi complessivo è il seguente:
L’applicazione WPF riportata in allegato ha la semplice interfaccia:
Da notare che la visualizzazione delle soluzioni (di fatto dei Complex?) è eseguita grazie al metodo di estensione:
- <Extension()>
- Public Function Format(ByVal c As Complex?) As String
- Dim retStrBuild = New StringBuilder
- If c.HasValue Then
- If c.Value.Real = 0 Then
- If c.Value.Imaginary = 0 Then
- retStrBuild.Append("0")
- Else
- retStrBuild.AppendFormat("{0:F4} i", c.Value.Imaginary)
- End If
- Else
- retStrBuild.AppendFormat("{0:F4}", c.Value.Real)
- If c.Value.Imaginary > 0 Then
- retStrBuild.AppendFormat(" + {0:F4} i", c.Value.Imaginary)
- ElseIf c.Value.Imaginary < 0 Then
- retStrBuild.AppendFormat(" - {0:F4} i", Math.Abs(c.Value.Imaginary))
- End If
- End If
- Else
- retStrBuild.Append("-")
- End If
- Return retStrBuild.ToString()
- End Function
Il codice completo della solution è scaricabile dal seguente link:


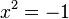

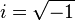



Commenti